与两异面直线垂直相交的直线为什么只有一个
两条
异面直线
只有一条公垂线,直线外一点可能在此异面直线公垂线上,也可能在公垂线外。在公垂线上此公垂线就为过改点与两直线都垂直的线(1条),若不在公垂线上那么就找不到第二条直线过改点与两异面直线垂直(0条)(原因:公垂线只有一条公垂线)。所以过两条异面直线外一点
与两直线都垂直的线有0或1条。

与两异面直线垂直相交的直线
不同在任何一个平面内的两条直线叫做异面直线。
特点:既不平行,也不相交。
判定方法:(1)定义法:由定义判定两直线永远不可能在同一平面内。
(2)定理:过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线。两条异面直线所成的角的定义:直线a,b是异面直线,经过空间一点O,分别引直线A//a,B//b,相交直线A,B所成的锐角(或直角)叫做异面直线a,b所成的角。
两条异面直线垂直的定义:如果两条异面直线所成的角是直角,则称这两条异面直线互相垂直。两条异面直线的公垂线的定义:和两条异面直线都垂直相交的直线叫做两条异面直线的公垂线。两条异面直线的距离的定义:两条异面直线的公垂线在这两条异面直线间的线段,叫做这两条异面直线的公垂线段;公垂线段的长度,叫做两条异面直线的距离。
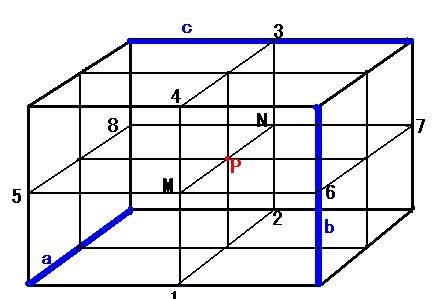
两个异面直线一定有公共法向量吗
就是公垂线拉,
只有公垂线才是跟两条异面直线都垂直.
就设公垂线坐标,
再与两条直线方向向量乘,
积为0,
解出就行
向量法:先求两异面直线得公共法向量,再求两异面直线上两点得连结线段在
公共法向量上得射影长。
例题
已知:正方体ABCD-A1B1C1D1得棱长为1,
求异面直线DA1与AC得距离。
思路分析:此题就是求异面直线得距离问题,这个距离可瞧作就是
在异面直线得法向量方向上得投影得绝对值。
此题教师引导,学生口述,教师在课件上演示解题
过程,总结解题步骤。
两条直线异面垂直能推出什么结论
异面直线证平行和垂直方法:根据“一条直线垂直于一个平面,则这条直线与这个平面上的所有直线都垂直”。
如果一条直线垂直于另一条直线所在的平面,则这两条异面直线垂直。如果两条异面直线所成的角是直角,则称这两条异面直线互相垂直。不同在任何一个平面内的两条直线叫做异面直线
两条直线垂直包不包括异面
在立体几何中,两条直线垂直,那么这两条直线可能共面也可能异面!两条直线异面,那么这两条直线可能垂直也可能不垂直!所谓异面直线垂直是指两条直线平移到同一平面后垂直!
异面和垂直有什么区别和联系
异面和垂直有区别和联系为
异面
异面直线是不在同一平面上的两条直线。异面直线是既不相交,又不平行的直线。因为两条直线如果相交或平行,则它们必在同一平面上。若无特别的说明,所说的空间直线,都是指异面直线。
垂直
垂直,是指一条线与另一条线成直角,这两条直线互相垂直。通常用符号“⊥”表示。
设有两个向量a和b,a⊥b的充要条件是a·b=0,即(x1x2+y1y2)=0 。
对于立体几何中的垂直问题,主要涉及到线面垂直问题与面面垂直问题,而要解决相关的问题,其难点是线面垂直的定义及其对判定定理成立的条件的理解;两平面垂直的判定定理及其运用和对二面角有关概念的理解。
异面垂直判定定理
异面直线证平行和垂直方法:
根据“一条直线垂直于一个平面,则这条直线与这个平面上的所有直线都垂直”。
如果一条直线垂直于另一条直线所在的平面,则这两条异面直线垂直。
如果两条异面直线所成的角是直角,则称这两条异面直线互相垂直。
不同在任何一个平面内的两条直线叫做异面直线。
异面直线判定方法:
定义法:由定义判定两直线永远不可能在同一平面内。
定理:经过平面外一点和平面内一点的直线和平面内不经过该点的直线,是异面直线。
版权声明:本文来自用户投稿,不代表【匆匆网】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:dandanxi6@qq.com)我们将及时处理,共同维护良好的网络创作环境。








